Convex and Concave Dispositions
2020 Nov 08
See all posts
Convex and Concave Dispositions
One of the major philosophical differences that I have noticed in how people approach making large-scale decisions in the world is how they approach the age-old tradeoff of compromise versus purity. Given a choice between two alternatives, often both expressed as deep principled philosophies, do you naturally gravitate toward the idea that one of the two paths should be correct and we should stick to it, or do you prefer to find a way in the middle between the two extremes?
In mathematical terms, we can rephrase this as follows: do you expect the world that we are living in, and in particular the way that it responds to the actions that we take, to fundamentally be concave or convex?
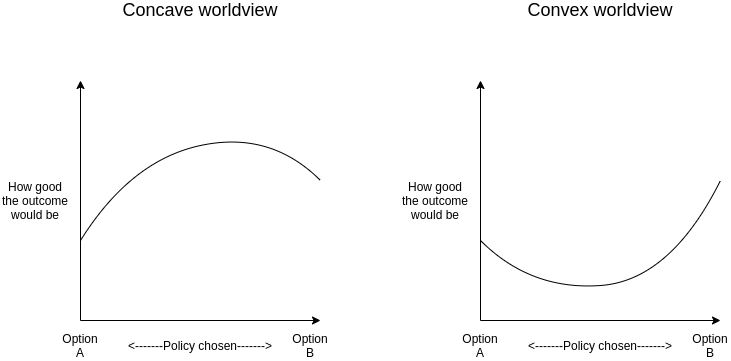
Someone with a concave disposition might say things like this:
- "Going to the extremes has never been good for us; you can die from being too hot or too cold. We need to find the balance between the two that's just right"
- "If you implement only a little bit of a philosophy, you can pick the parts that have the highest benefits and the lowest risks, and avoid the parts that are more risky. But if you insist on going to the extremes, once you've picked the low-hanging fruit, you'll be forced to look harder and harder for smaller and smaller benefits, and before you know it the growing risks might outweigh the benefit of the whole thing"
- "The opposing philosophy probably has some value too, so we should try to combine the best parts of both, and definitely avoid doing things that the opposing philosophy considers to be extremely terrible, just in case"
Someone with a convex disposition might say things like this:
- "We need to focus. Otherwise, we risk becoming a jack of all trades, master of none"
- "If we take even a few steps down that road, it will become slippery slope and only pull us down ever further until we end up in the abyss. There's only two stable positions on the slope: either we're down there, or we stay up here"
- "If you give an inch, they will take a mile"
- "Whether we're following this philosophy or that philosophy, we should be following some philosophy and just stick to it. Making a wishy-washy mix of everything doesn't make sense"
I personally find myself perenially more sympathetic to the concave approach than the convex approach, across a wide variety of contexts. If I had to choose either (i) a coin-flip between anarcho-capitalism and Soviet communism or (ii) a 50/50 compromise between the two, I would pick the latter in a heartbeat. I argued for moderation in Bitcoin block size debates, arguing against both 1-2 MB small blocks and 128 MB "very big blocks". I've argued against the idea that freedom and decentralization are "you either have it or you don't" properties with no middle ground. I argued in favor of the DAO fork, but to many people's surprise I've argued since then against similar "state-intervention" hard forks that were proposed more recently. As I said in 2019, "support for Szabo's law [blockchain immutability] is a spectrum, not a binary".
But as you can probably tell by the fact that I needed to make those statements at all, not everyone seems to share the same broad intuition. I would particularly argue that the Ethereum ecosystem in general has a fundamentally concave temperament, while the Bitcoin ecosystem's temperament is much more fundamentally convex. In Bitcoin land, you can frequently hear arguments that, for example, either you have self-sovereignty or you don't, or that any system must have either a fundamentally centralizing or a fundamentally decentralizing tendency, with no possibility halfway in between.
The occasional half-joking support for Tron is a key example: from my own concave point of view, if you value decentralization and immutability, you should recognize that while the Ethereum ecosystem does sometimes violate purist conceptions of these values, Tron violates them far more egregiously and without remorse, and so Ethereum is still by far the more palatable of the two options. But from a convex point of view, the extremeness of Tron's violations of these norms is a virtue: while Ethereum half-heartedly pretends to be decentralized, Tron is centralized but at least it's proud and honest about it.
This difference between concave and convex mindsets is not at all limited to arcane points about efficiency/decentralization tradeoffs in cryptocurrencies. It applies to politics (guess which side has more outright anarcho-capitalists), other choices in technology, and even what food you eat.
But in all of these questions too, I personally find myself fairly consistently coming out on the side of balance.
Being concave about concavity
But it's worth noting that even on the meta-level, concave temperament is something that one must take great care to avoid being extreme about. There are certainly situations where policy A gives a good result, policy B gives a worse but still tolerable result, but a half-hearted mix between the two is worst of all. The coronavirus is perhaps an excellent example: a 100% effective travel ban is far more than twice as useful as a 50% effective travel ban. An effective lockdown that pushes the R0 of the virus down below 1 can eradicate the virus, leading to a quick recovery, but a half-hearted lockdown that only pushes the R0 down to 1.3 leads to months of agony with little to show for it. This is one possible explanation for why many Western countries responded poorly to it: political systems designed for compromise risk falling into middle approaches even when they are not effective.
Another example is a war: if you invade country A, you conquer country A, if you invade country B, you conquer country B, but if you invade both at the same time sending half your soldiers to each one, the power of the two combined will crush you. In general, problems where the effect of a response is convex are often places where you can find benefits of some degree of centralization.
But there are also many places where a mix is clearly better than either extreme. A common example is the question of setting tax rates. In economics there is the general principle that deadweight loss is quadratic: that is, the harms from the inefficiency of a tax are proportional to the square of the tax rate. The reason why this is the case can be seen as follows. A tax rate of 2% deters very few transactions, and even the transactions it deters are not very valuable - how valuable can a transaction be if a mere 2% tax is enough to discourage the participants from making it? A tax rate of 20% would deter perhaps ten times more transactions, but each individual transaction that was deterred is itself ten times more valuable to its participants than in the 2% case. Hence, a 10x higher tax may cause 100x higher economic harm. And for this reason, a low tax is generally better than a coin flip between high tax and no tax.
By similar economic logic, an outright prohibition on some behavior may cause more than twice as much harm as a tax set high enough to only deter half of people from participating. Replacing existing prohibitions with medium-high punitive taxes (a very concave-temperamental thing to do) could increase efficiency, increase freedom and provide valuable revenue to build public goods or help the impoverished.
Another example of effects like this in Laffer curve: a tax rate of zero raises no revenue, a tax rate of 100% raises no revenue because no one bothers to work, but some tax rate in the middle raises the most revenue. There are debates about what that revenue-maximizing rate is, but in general there's broad agreement that the chart looks something like this:
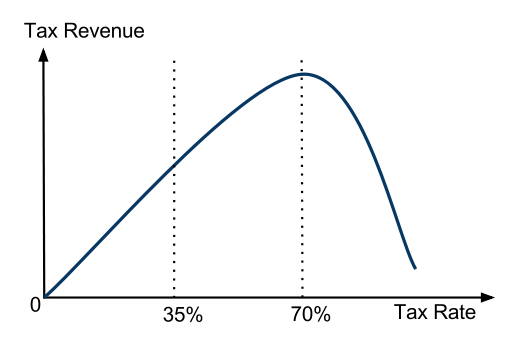
If you had to pick either the average of two proposed tax plans, or a coin-flip between them, it's obvious that the average is usually best. And taxes are not the only phenomenon that are like this; economics studies a wide array of "diminishing returns" phenomena which occur everywhere in production, consumption and many other aspects of regular day-to-day behavior. Finally, a common flip-side of diminishing returns is accelerating costs: to give one notable example, if you take standard economic models of utility of money, they directly imply that double the economic inequality can cause four times the harm.
The world has more than one dimension
Another point of complexity is that in the real world, policies are not just single-dimensional numbers. There are many ways to average between two different policies, or two different philosophies. One easy example to see this is: suppose that you and your friend want to live together, but you want to live in Toronto and your friend wants to live in New York. How would you compromise between these two options?
Well, you could take the geographic compromise, and enjoy your peaceful existence at the arithmetic midpoint between the two lovely cities at....
This Assembly of God church about 29km southwest of Ithaca, NY.
Or you could be even more mathematically pure, and take the straight-line midpoint between Toronto and New York without even bothering to stay on the Earth's surface. Then, you're still pretty close to that church, but you're six kilometers under it. A different way to compromise is spending six months every year in Toronto and six months in New York - and this may well be an actually reasonable path for some people to take.
The point is, when the options being presented to you are more complicated than simple single-dimensional numbers, figuring out how to compromise between the options well, and really take the best parts of both and not the worst parts of both, is an art, and a challenging one.
And this is to be expected: "convex" and "concave" are terms best suited to mathematical functions where the input and the output are both one-dimensional. The real world is high-dimensional - and as machine-learning researchers have now well established, in high-dimensional environments the most common setting that you can expect to find yourself in is not a universally convex or universally concave one, but rather a saddle point: a point where the local region is convex in some directions but concave in other directions.

A saddle point. Convex left-to-right, concave forward-to-backward.
This is probably the best mathematical explanation for why both of these dispositions are to some extent necessary: the world is not entirely convex, but it is not entirely concave either. But the existence of some concave path between any two distant positions A and B is very likely, and if you can find that path then you can often find a synthesis between the two positions that is better than both.
Convex and Concave Dispositions
2020 Nov 08 See all postsOne of the major philosophical differences that I have noticed in how people approach making large-scale decisions in the world is how they approach the age-old tradeoff of compromise versus purity. Given a choice between two alternatives, often both expressed as deep principled philosophies, do you naturally gravitate toward the idea that one of the two paths should be correct and we should stick to it, or do you prefer to find a way in the middle between the two extremes?
In mathematical terms, we can rephrase this as follows: do you expect the world that we are living in, and in particular the way that it responds to the actions that we take, to fundamentally be concave or convex?
Someone with a concave disposition might say things like this:
Someone with a convex disposition might say things like this:
I personally find myself perenially more sympathetic to the concave approach than the convex approach, across a wide variety of contexts. If I had to choose either (i) a coin-flip between anarcho-capitalism and Soviet communism or (ii) a 50/50 compromise between the two, I would pick the latter in a heartbeat. I argued for moderation in Bitcoin block size debates, arguing against both 1-2 MB small blocks and 128 MB "very big blocks". I've argued against the idea that freedom and decentralization are "you either have it or you don't" properties with no middle ground. I argued in favor of the DAO fork, but to many people's surprise I've argued since then against similar "state-intervention" hard forks that were proposed more recently. As I said in 2019, "support for Szabo's law [blockchain immutability] is a spectrum, not a binary".
But as you can probably tell by the fact that I needed to make those statements at all, not everyone seems to share the same broad intuition. I would particularly argue that the Ethereum ecosystem in general has a fundamentally concave temperament, while the Bitcoin ecosystem's temperament is much more fundamentally convex. In Bitcoin land, you can frequently hear arguments that, for example, either you have self-sovereignty or you don't, or that any system must have either a fundamentally centralizing or a fundamentally decentralizing tendency, with no possibility halfway in between.
The occasional half-joking support for Tron is a key example: from my own concave point of view, if you value decentralization and immutability, you should recognize that while the Ethereum ecosystem does sometimes violate purist conceptions of these values, Tron violates them far more egregiously and without remorse, and so Ethereum is still by far the more palatable of the two options. But from a convex point of view, the extremeness of Tron's violations of these norms is a virtue: while Ethereum half-heartedly pretends to be decentralized, Tron is centralized but at least it's proud and honest about it.
This difference between concave and convex mindsets is not at all limited to arcane points about efficiency/decentralization tradeoffs in cryptocurrencies. It applies to politics (guess which side has more outright anarcho-capitalists), other choices in technology, and even what food you eat.
But in all of these questions too, I personally find myself fairly consistently coming out on the side of balance.
Being concave about concavity
But it's worth noting that even on the meta-level, concave temperament is something that one must take great care to avoid being extreme about. There are certainly situations where policy A gives a good result, policy B gives a worse but still tolerable result, but a half-hearted mix between the two is worst of all. The coronavirus is perhaps an excellent example: a 100% effective travel ban is far more than twice as useful as a 50% effective travel ban. An effective lockdown that pushes the R0 of the virus down below 1 can eradicate the virus, leading to a quick recovery, but a half-hearted lockdown that only pushes the R0 down to 1.3 leads to months of agony with little to show for it. This is one possible explanation for why many Western countries responded poorly to it: political systems designed for compromise risk falling into middle approaches even when they are not effective.
Another example is a war: if you invade country A, you conquer country A, if you invade country B, you conquer country B, but if you invade both at the same time sending half your soldiers to each one, the power of the two combined will crush you. In general, problems where the effect of a response is convex are often places where you can find benefits of some degree of centralization.
But there are also many places where a mix is clearly better than either extreme. A common example is the question of setting tax rates. In economics there is the general principle that deadweight loss is quadratic: that is, the harms from the inefficiency of a tax are proportional to the square of the tax rate. The reason why this is the case can be seen as follows. A tax rate of 2% deters very few transactions, and even the transactions it deters are not very valuable - how valuable can a transaction be if a mere 2% tax is enough to discourage the participants from making it? A tax rate of 20% would deter perhaps ten times more transactions, but each individual transaction that was deterred is itself ten times more valuable to its participants than in the 2% case. Hence, a 10x higher tax may cause 100x higher economic harm. And for this reason, a low tax is generally better than a coin flip between high tax and no tax.
By similar economic logic, an outright prohibition on some behavior may cause more than twice as much harm as a tax set high enough to only deter half of people from participating. Replacing existing prohibitions with medium-high punitive taxes (a very concave-temperamental thing to do) could increase efficiency, increase freedom and provide valuable revenue to build public goods or help the impoverished.
Another example of effects like this in Laffer curve: a tax rate of zero raises no revenue, a tax rate of 100% raises no revenue because no one bothers to work, but some tax rate in the middle raises the most revenue. There are debates about what that revenue-maximizing rate is, but in general there's broad agreement that the chart looks something like this:
If you had to pick either the average of two proposed tax plans, or a coin-flip between them, it's obvious that the average is usually best. And taxes are not the only phenomenon that are like this; economics studies a wide array of "diminishing returns" phenomena which occur everywhere in production, consumption and many other aspects of regular day-to-day behavior. Finally, a common flip-side of diminishing returns is accelerating costs: to give one notable example, if you take standard economic models of utility of money, they directly imply that double the economic inequality can cause four times the harm.
The world has more than one dimension
Another point of complexity is that in the real world, policies are not just single-dimensional numbers. There are many ways to average between two different policies, or two different philosophies. One easy example to see this is: suppose that you and your friend want to live together, but you want to live in Toronto and your friend wants to live in New York. How would you compromise between these two options?
Well, you could take the geographic compromise, and enjoy your peaceful existence at the arithmetic midpoint between the two lovely cities at....
This Assembly of God church about 29km southwest of Ithaca, NY.
Or you could be even more mathematically pure, and take the straight-line midpoint between Toronto and New York without even bothering to stay on the Earth's surface. Then, you're still pretty close to that church, but you're six kilometers under it. A different way to compromise is spending six months every year in Toronto and six months in New York - and this may well be an actually reasonable path for some people to take.
The point is, when the options being presented to you are more complicated than simple single-dimensional numbers, figuring out how to compromise between the options well, and really take the best parts of both and not the worst parts of both, is an art, and a challenging one.
And this is to be expected: "convex" and "concave" are terms best suited to mathematical functions where the input and the output are both one-dimensional. The real world is high-dimensional - and as machine-learning researchers have now well established, in high-dimensional environments the most common setting that you can expect to find yourself in is not a universally convex or universally concave one, but rather a saddle point: a point where the local region is convex in some directions but concave in other directions.
A saddle point. Convex left-to-right, concave forward-to-backward.
This is probably the best mathematical explanation for why both of these dispositions are to some extent necessary: the world is not entirely convex, but it is not entirely concave either. But the existence of some concave path between any two distant positions A and B is very likely, and if you can find that path then you can often find a synthesis between the two positions that is better than both.